Statistical significance testing
Published:
In recent blog posts I have described many potential issues with MT evaluation. Surely statistical significance testing should help mitigate some of those problems? That may seem reasonable, but the truth is: it can be laughably easy to arrive at results that are statistically significant according to the most popular test in MT research, bootstrap resampling.
Papers on MT routinely compute statistical significance, mostly using Philipp Koehn’s bootstrap resampling method (Koehn, 2004). In a nutshell, bootstrap resampling means to
Translate a test set with N sentences once , say N=300 (used in the original paper)
Sample N pairs of (hypothesis, reference) with replacement from the translations by our system and the reference translations. Repeat this experiment X times, say X=1000. We will end up with 1000 different test sets.
For each of those X test sets, compute our test metric, e.g. BLEU score. This gives us a distribution over BLEU scores that can be used as a substitute for translating and evaluating a very large number of sentences that is more representative of all possible sentences.
A variant called “paired bootstrap” is used to actually compare systems with each other. It basically computes which system performed better in X trials with X sampled test sets.
As you can see, it’s a test that accounts for sampling variation in the test set. That is certainly important, but it hinges on the assumption that the test set distribution is representative of the distribution in the entire “population” of target language (Dror et al., 2018). That might not be a problem, but the following is: bootstrap resampling does not account for random variation across training runs. This means that while it may be true that two models are significantly different, the difference might not be due to the “treatment” applied (e.g. increase number of encoder layers) but due to randomness.
Anecdotally, many people have found that in all but few cases, paired bootstrap reports that there is a difference between systems. It is possible that this is precisely because of variation caused by random seeds. In other words, what happens if paired bootstrap is comparing two models that differ only in their random seed? For your convenience I did a quick test — the code and results are available. The main outcome is: one of the systems is superior with p=0.03 , which is worrying given that so often p<0.05 is described as as a meaningful cutoff.
I concede that there are situations where significance testing for MT is useful, if other methods are not feasible. Imagine a decision chart such as this one:
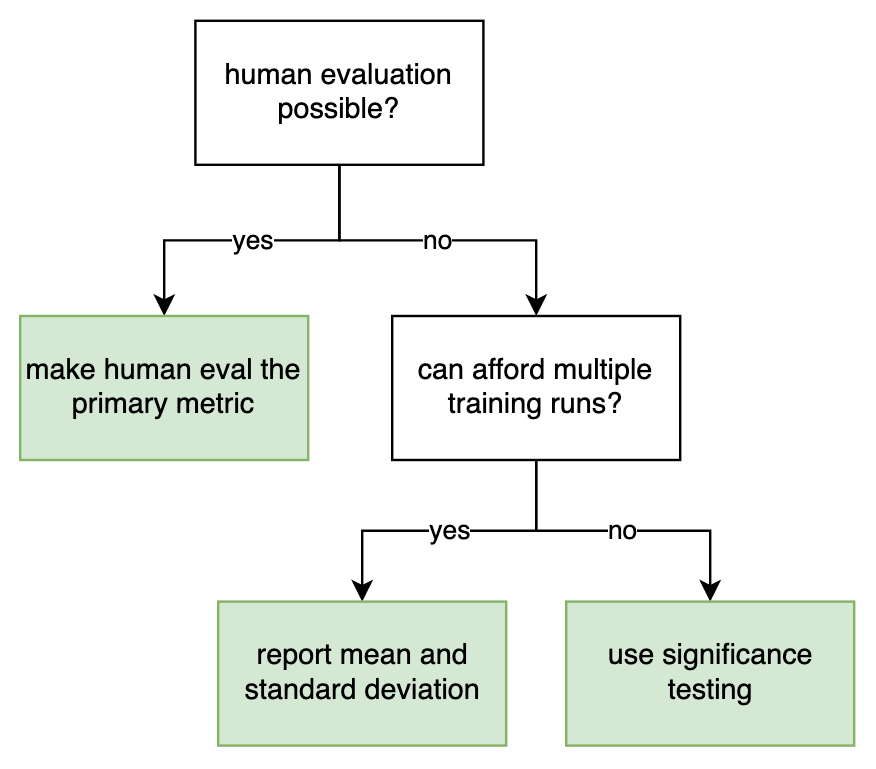
If several training runs and human evaluation are not feasible, then using a significance test for automatic estimates of translation quality may well be the best thing to do.
Recommendation
Don’t rely too much on statistical significance testing for metrics of translation quality. Focus on gains in automatic translation quality beyond standard deviation, or ideally human evaluation.
FAQ
Q: Paired bootstrap is actually not the only significance test. For instance, approximate randomization can be used as well!
Yes, that is true. But in MT at least, several tests (including paired bootstrap and approximate randomization) appear to lead to the same conclusions (Graham et al., 2014).
Q: I would like to use significance tests properly, but they are not integrated into any popular toolkit or framework I know.
Update: As of version 2.0, SacreBLEU offers bootstrap resampling and approximate randomization!
Other than that, there are no good options here except slow, isolated scripts or in outdated frameworks.
